|
|
|
|
|
|
|
| HARDWARE | DOWNLOADS | MISCELLANEOUS | ||||
|
|
|
 |
|
|
 | |  |
 |
FBUS & M2BUS | ||||
|
|
PanuWorld project:
Miniature 3 V FBUS/M2BUS to V.24 adapter using MAX232
CAUTION: These old FBUS & M2BUS adapters are now superseded by the new FBUS & M2BUS adapters. This page is saved only as a reference.
The main reason for PanuWorld to begin Nokia phone data cables was the fact that all circuits published in the web where based on the MAX3232. This chip was hard to find and the prices were something around FIM 40 (6.73
). MAX232 was sold at FIM 5 (0.84
I found several problems that should have been solved in the adapters (table 1).
Table 1. The first problems with the MAX232 in a PC - Nokia phone adapter.
The output voltage of the adapter in the 3 V port.
- Because the MAX232 is run at 5 V, the high state of the MAX TTL/CMOS output is near 5 volts. The output level is limited here with a resistor-zener diode limiter. This affects the maximum speed of the data. Other problems are also possible: If the adapter output is connected to the M2BUS pin of the phone, the internal 5-kilo-ohm pull-up of the phone creates a voltage divider with the limiter resistor when the adapter output should be "0". So the value of the limiter resistor is critical.
- The high level in the best case is about 3 volts in the adapter input driven by the 3-volt-equipment. In worst case it can be 1.5 volts, but this is not probable. (No specification of the output of a Nokia 5100/6100 phone is not known.) The data sheets of MAX232 show that with a power supply of 5 V ± 10% the maximum value for minimum input level understood to be "high" is 2.0 volts. This 2.0-volt-limit is probably fulfilled by the 3 V device (phone).
- The nominal power supply current of MAX232 without any loads is 4 mA, but with the MAX3232 it is 0.3 mA. Because the V.24 port output levels are higher in MAX232 than in MAX3232 the power dissipation in the line termination is also higher. There are problems to get enough power to the chip. The supply voltage drops easily below 5 - 10% volts because too much current is drawn.
- Many of the circuit designs available on the Internet connect only the FBUS port to the V.24. Basically also the M2BUS support is easy to implement, but if no switches are allowed, undisturbed transmission with both methods is difficult with MAX232. The dual-mode cable described in this document uses a special RTS controlled soft-switch to switch between the FBUS and M2BUS modes. It seems to be that the V.24 RTS (Ready To Send) circuit is used in the Nokia software to tell if the M2BUS is in use.
The original PanuWorld adapter where "FBUS-only" and "Dual-mode" (FBUS & M2BUS support with a bipolar transistor switch). These circuits are shown in figures 1 and 2.
Figure 1. Miniature 3 V FBUS to V.24 adapter using MAX232 (FBUS-only).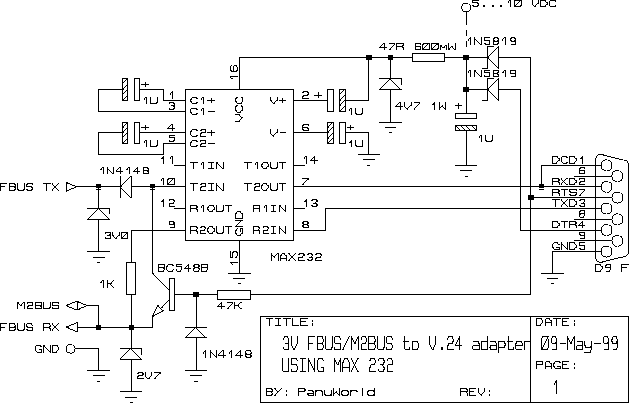
Figure 2. Miniature 3 V FBUS & M2BUS to V.24 adapter using MAX232 (dual-mode).There were several uncertainties in the old adapters. These problems were:
- The VCC voltage of the MAX232 was usually not the specifications (5 V ± 10%). The reason was the high power consumption and the voltage drop in computer's serial port drivers and in the 47-ohm resistor of the zener regulator sub-circuit.
- The FBUS Tx floats when the FBUS is idle, so the T2IN input must be pulled up to ensure proper RxD state. The T2IN is internally pulled up with a 400 kilo-ohm resistor, but the problem was the reverse leakage current of the 3 V zener diode that pulled the T2IN input to a bad "middle" state.
- The reverse current of the 2.7 V zener loaded the phone inputs and prevented using a diode to form an open-collector compatible output for the R2OUT.
For example, Nokia 5110 and Nokia 6110 are 5100/6100 series phones. The tests have been done with Nokia Data Suite 2.0 application and a Nokia 6110 phone. No exact information about compatibility with others is known.
9.1.2001
Email replies cannot be guaranteed.